SCoRe: Submodular Combinatorial Representation Learning

Anay Majee1, Suraj Kothawade2, Krishnateja Killamsetty3, Rishabh Iyer1,
1The University of Texas at Dallas , 2Google Research , 3IBM Research
ICML 2024
Paper Code arXiv
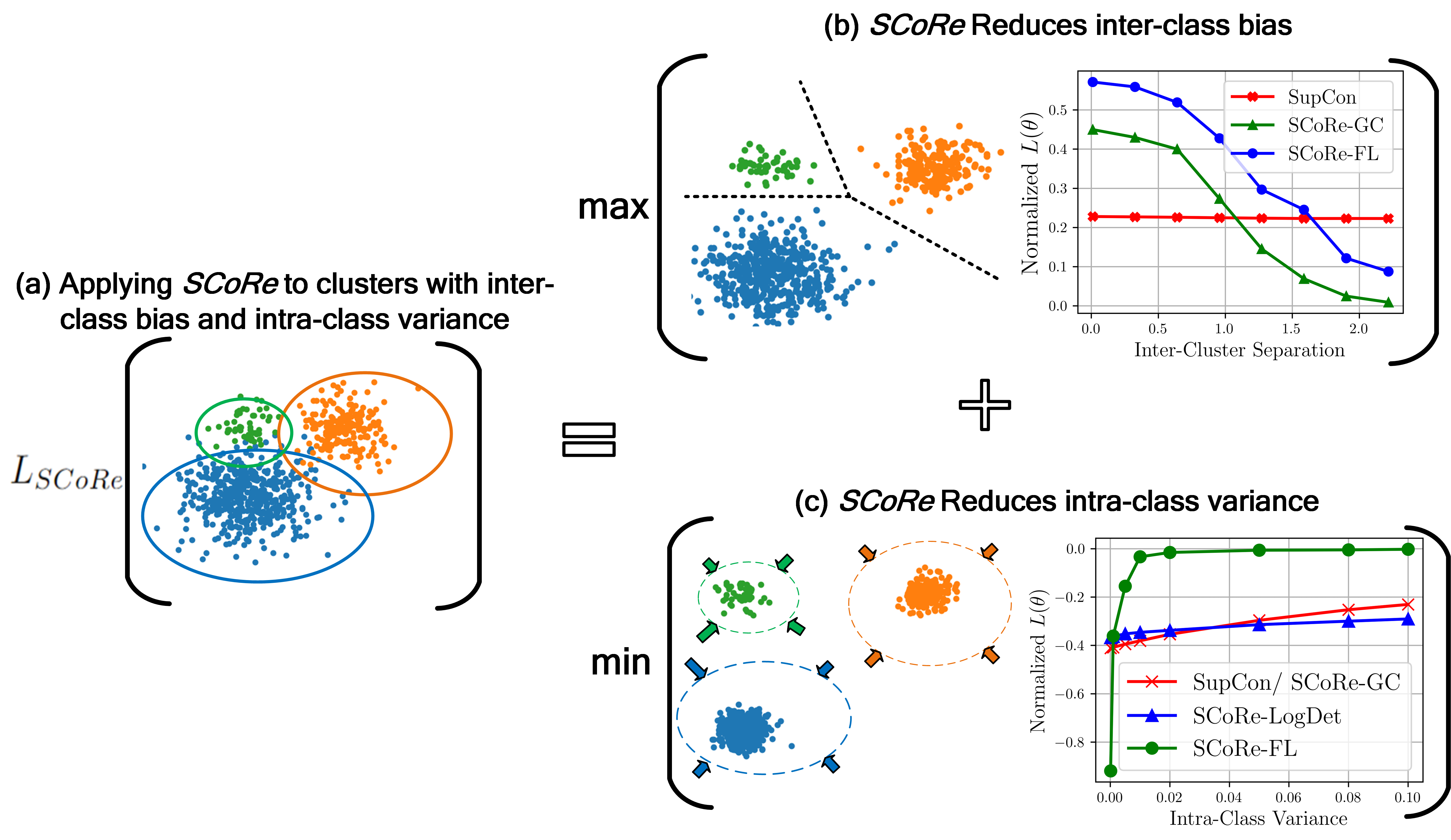
MY ALT TEXT

SCoRe introduces a family of Submodular combinatorial objectives designed to tackle the challenge of inter-class bias (b) and intra-class variance (c) demonstrated in Long-tail recognition tasks.

Abstract

In this paper we introduce the SCoRe (Submodular Combinatorial Representation Learning) framework, a novel approach in machine vision representation learning that addresses inter-class bias and intra-class variance. SCoRe provides a new combinatorial viewpoint to representation learning, by introducing a family of loss functions based on set-based submodular information measures. We craft two novel combinatorial formulations for loss functions, that model Total Information and Total Correlation, that naturally minimize intra-class variance and inter-class bias. Several commonly used metric/contrastive learning loss functions like supervised contrastive loss, orthagonal projection loss, and N-pairs loss, are all instances of SCoRe, thereby underlining the versatility and applicability of SCoRe in a broad spectrum of learning scenarios. Novel objectives in SCoRe naturally model class-imbalance with up to 7.6% improvement in classification on CIFAR-10-LT, CIFAR-100-LT, MedMNIST, 2.1% on ImageNet-LT, and 19.4% in object detection on IDD and LVIS (v1.0), demonstrating its effectiveness over existing approaches.

Inter-Class Bias and Intra-Class variance in Long-tail Recognition

Long-tail recognition encompasses both imbalanced and few-shot classification tasks in the presence of both abundant (head) and rare (tail) classes in the data distribution. This introduces a natural bias towards the abundant classes and large variance within each abundant class in models trained on such distributions. Representation learning in this space requires a model to learn discriminative features not only from the abundant classes but also from the rare ones. Unfortunately, models trained on real-world datasets demonstrate two main challenges - inter-class bias and intra-class variance resulting in overlapping clusters alongside large cluster variance.

Inter-Class bias manifests itself as mis-predictions in rare classes being predicted as one or more of the visually similar abundant classes. This mis-prediction results from the bias existng in the trained model, towards the abundant classes demostrating cluster overlaps between head and tail classes in the embedding space as shown in the figure below.

Inter-Class Variance

Figure 1: Resilience to inter-class variance by objectives in SCoRe. SCoRe objectives like SCoRe-FL show a large variation to intra-class variance over SoTA approaches like SupCon.



Intra-Class Variance manifests itself as the large variance within each class (see below figure) resulting in cluster overlaps between abundannt and rare classes. It also manifests itself as creation of local sub-centers intensifying the bias of the underlying model towards the head classes resulting in poor performance on the tail classes.

Intra-Class Variance

Figure 2: Resilience to intra-class variance by objectives in SCoRe. SCoRe objectives like SCoRe-FL show a large variation to intra-class variance over SoTA approaches like SupCon.



Thus, a model trained on long-tail distributions must learn discriminative representations for each class, minimizing the effect of inter-class bias and intra-class variance.

Submodular Combinatorial Loss Functions


SCoRe introduces a combinatorial viewpoint by defining a dataset \(\mathcal{T}\) as a collection of sets, \(\mathcal{T} = \{A_1,A_2, \cdots, A_{|C|}\}\) over classes (now represented as sets \(A_k\)) in \(\mathcal{T}\). Submodular Information functions are set-based (combinatorial) information theoretic functions which inherently model the properties of diversity and cooperatiion. Minimizing a submodular function over a set \(A_k\) reduces cluster variance by modelling cooperation between samples in a set thereby reducing intra-class variance. Maximizing a submodular function over all sets in the dataset (\(\cup_{k=1}^{|C|} A_k\)) models diversity between sets resulting in increased inter-cluater separation, reducing the impact of inter-class bias.

Designing Combinatorial Losses for Long-tail Recognition

Modelling the properties of diversity and cooperation by submodular functions we derive two novel formulations.

Longtail boat in Thailand

Figure 3 : Combinatorial Objectives and generalization to existing metric/contrastive learners.

Total Information (\(L_{S_f}\)) models the total submodular information contained in a set \(A_{k}\). Minimizing the total information models cooperation resulting in low intra-class variance.

Total Correlation (\(L_{C_f}\)) models the gain in information in set \(A_k\) when new information is added to the set. This formulation shown below, encapsulates the total information alongside a diversity term over the complete dataset which minimizes inter-cluster overlap. \[L_{S_f} = \overset{|C|}{\underset{k=1}{\sum}} \frac{1}{N_f(A_k)}\,\,f(A_k; \theta) \,\,\, ; \,\,\, L_{C_f} = \overset{|C|}{\underset{k=1}{\sum}} \frac{1}{N_f(A_k)}\,\, \Biggl[f(A_k; \theta) - f(\overset{|C|}{\underset{k=1}{\cup}}A_k; \theta)\Biggr]\]


The Total Correlation formulation thus models both inter-class bias and intra-class variance, minimizing which results in learning of dicriminative representations in long-tail settings.

It is interesting to note that existing approaches in metric/ contrastive learning arre either instances of SCoRe or can be re-formulated into instances SCoRe. Following existing approaches, we adopt pairwise simialrity to model interactions between samples but differ in aggregation of the similarity kernel to compute total information / correlation. Depending on the choice of Submodular function \(f(A_k ; \theta)\) we define a family of loss functions as shown in Table 1 below.

Table 1 : Summary of family of Objectives in SCoRe and their respective combinatorial properties.

\[\begin{array}{l|c|c} \hline \textbf{Objective Function} & \textbf{Equation \(L(\theta)\)}& \textbf{Combinatorial} \\ & & \textbf{Property}\\ \hline \hline \text{Triplet Loss} & \sum_{k = 1}^{|C|}\frac{1}{|A_k|}[ \sum_{\substack{i,p \in A_{k}, \\ n \in \mathcal{V} \setminus A_{k}}} \max (0, D_{ip}^2(\theta) - D_{in}^2(\theta) + \epsilon)] & \text{Not Submodular} \\ & & \\ \text{SNN} & \sum_{k = 1}^{|C|}\frac{-1}{|A_k|}\sum_{i \in A_{k}} {\log \sum_{j \in A_{k}} \exp(S_{ij}(\theta)) + \frac{1}{|A_k|} \log\sum_{\substack{i \in A_{k} \\ j \in \mathcal{V} \setminus A_{k}}} \exp(S_{ij}(\theta))} & \text{Not Submodular} \\ & & \\ \hline \text{N-Pairs Loss} & \sum_{k = 1}^{|C|} \frac{-1}{|A_k|}{\sum_{i,j \in A_{k}} S_{ij}(\theta) + \frac{1}{|A_k|}\sum_{i \in A_{k}} log(\sum_{j \in \mathcal{V}} S_{ij}(\theta) - 1)} & \text{Submodular} \\ & & \\ \text{OPL} & \sum_{k = 1}^{|C|} \frac{1}{|A_k|}( 1 - \sum_{i,j \in A_{k}} S_{ij}(\theta)) + \frac{1}{|A_k|}\sum_{i \in A_{k}} \sum_{j \in \mathcal{V} \setminus A_{k}} S_{ij}(\theta) & \text{Submodular} \\ & & \\ \text{SupCon} & \sum_{k = 1}^{|C|} [\frac{-1}{|A_{k}|} \sum_{i,j \in A_{k}} S_{ij}(\theta) ] + \sum_{i \in A_{k}}\frac{1}{|A_{k}|}\log(\sum_{j \in V}exp(S_{ij}(\theta)) - 1) & \text{Submodular} \\ & & \\ \hline \text{Submod-Triplet} & \sum_{k = 1}^{|C|} \frac{1}{|A_k|}\sum_{\substack{i \in A_{k} \\ n \in \mathcal{V} \setminus A_{k}}} S_{in}^{2}(\theta) - \sum_{i,p \in A} S_{ip}^{2}(\theta) & \text{Submodular} \\ & & \\ \text{Submod-SNN} & \sum_{k = 1}^{|C|} \frac{1}{|A_k|}\sum_{i \in A_{k}} [\log \sum_{j \in A_{k}} \exp(D_{ij}(\theta)) + \log\sum_{j \in \mathcal{V} \setminus A_{k}} \exp(S_{ij}(\theta))] & \text{Submodular} \\ & & \\ \text{SupCon-Var} & \sum_{k = 1}^{|C|} \frac{-1}{|A_k|}{\sum_{i,j \in A_{k}} S_{ij}(\theta) + \frac{1}{|A_k|}\sum_{i \in A_{k}} log \sum_{j \in \mathcal{V} \setminus A_{k}} \exp(S_{ij}(\theta))} & \text{Submodular} \\ & & \\ \hline \text{SCoRe-GC} [S_f] (ours) & \sum_{k = 1}^{|C|} \frac{1}{|A_k|}[\sum_{i \in A_{k}}\sum_{j \in \mathcal{V} \setminus A_{k}}S_{ij}(\theta) - \lambda \sum_{i, j \in A_{k}} S_{ij}(\theta)] & \text{Submodular} \\ & & \\ \text{SCoRe-GC} [C_f] (ours) & \sum_{k = 1}^{|C|} \frac{\lambda}{|A_k|}\sum_{i \in A_{k}}\sum_{j \in \mathcal{V} \setminus A_{k}}S_{ij}(\theta) & \text{Submodular} \\ & & \\ \text{SCoRe-LogDet} [S_f] (ours) & \sum_{k = 1}^{|C|} \frac{1}{|A_k|}\log \det (S_{A_k}(\theta) + \lambda \mathbb{I}_{|A_k|}) & \text{Submodular} \\ & & \\ \text{SCoRe-LogDet} [C_f] (ours) & \sum_{k = 1}^{|C|} \frac{1}{|A_k|}[\log \det (S_{A_k}(\theta) + \lambda \mathbb{I}_{|A_k|}) - \log \det (S_{\mathcal{V}}(\theta) + \lambda \mathbb{I}_{|\mathcal{V}|})] & \text{Submodular} \\ & & \\ \text{SCoRe-FL} [C_{f}/ S_{f}] (ours) & \sum_{k = 1}^{|C|} \frac{1}{|\mathcal{V}|}\sum_{i \in \mathcal{V} \setminus A_{k}} max_{j \in A_{k}} S_{ij}(\theta) & \text{Submodular} \\ \hline \end{array}\]

What are the benefits of Adopting Combinatorial Objectives ?

Objectives introduced in SCoRe demonstrate some unique properties which deliver commendable benefits in learning dicriminative feature representations. Apart from results discussed in the paper we use synthetic data settings as shown in case 1 through 3 to demonstrate the effectives of SCoRe objectives under long-tail settings. From case 1 (base case) to case 2 we increase the variance of an abundant (head) cluster while from case 1 to case 3 we increase the variance of the tail class, both leading to increased overlaps and variance between clusters.

Bias and Variance in Long-Tail Recognition

Figure 4: Resilience to Intra-Class Variance and Inter-Class Bias under the Long-tail setting. Case 1 demonstrates no intra-class variance and inter-class bias, while case 2 demonstrates larger variance for the head class wile case 3 demonstrates larger variance for the tail class inducing inter-cluster overlaps.

Given these settings, we demonstrate the below properties:

  1. SCoRe Models Information in a Set The \(L_{S_f}\) formulation models the total information contained in a class (\(A_k\)) while the \(L_{C_f}\) formulation models the gain in information when new instances are added to \(A_k\). In contrast to existing losses that model sum over similarities or log-sum over similarities, objectives in SCoRe model information by aggregating pairwise interactions between samples.

  2. SCoRe-FL demonstrates inherent Class-balancing, equally weighting tail classes in contrast to head ones in model training. Unlike SoTA approaches that scale linearly with the cardinality of the set \(|A_k|\), SCoRe-FL has an inverse relation, and scales with respect to \(\mathcal{V}\setminus A_k\) (\(\sum_{i \in \mathcal{V} \setminus A_{k}} max_{j \in A_{k}} S_{ij}(\theta)\)). This inherently introduces class balancing critical in long-tail settings.

  3. SCoRe-LogDet models cluster volume by computing the volume of a feature cluster, minimizing which shrinks the cluster volume resulting in reduced intra-class variance (\(S_f\) form).

Results on Long-tail Recognition benchmarks

We perform experiments on several long-tail vision benchmarks to show the effectiveness of objectives in SCoRe towards learning of discriminative class-specific feature sets.

For Long-tail Recognition task we conduct experiments on CIFAR-10-LT, CIFAR-100-LT and ImageNet-LT. Following real-world benchmarks we introduce two new benchmarks - CIFAR-10-Step and the MedMNIST dataset which naturally model severe imbalance commonly observed in real-world data.

Applying our objectives demonstrate upto 4.3% in CIFAR-10-LT, 5.7% in CIFAR-100-LT and 2.1% in ImageNet-LT improvement over SoTA methods. We also show that our model converges relatively faster than SoTA metric/ contrastive learners demonstrating the benefits of adopting a set-based combinatorial viewpoint.

SoTA with SCoRe and Convergence

For Long-tail Object Detection we perform our experiments on two real-world benchmarks - LVIS (v1.0) and the India Driving Dataset. We demonstrate a 19.4% improvement in performance (\(mAP\)) for object detection tasks (in IDD).

Object Detection Results
More results on CIFAR-10-LT, CIFAR-100-LT and ImageNet-LT datasets are provided in our paper.

Citation

If you like our work or use it in your research please feel free to cite it based on the citation below. 

        @inproceedings{score,
          title = {SCoRe: Submodular Combinatorial Representation Learning},
          author = {Anay Majee and Suraj Kothawade and Krishnateja Killamsetty and Rishabh Iyer},
          booktitle = {ICML},
          year = {2024},
        }